写在前面:本文仅供学习交流使用,不构成任何投资建议!
前言
上一节我们介绍了均值回归的一些判断指标,下面我们来做一些简单的策略测试。
本文主要参考资料:”Algorithmic Trading: Winning Strategies and Their Rationale”, Ernest P. Chan
均值回归的线性交易策略
我们在此先直接使用均值回归的线性交易策略交易Bitcoin(即使根据我们前面的分析,这不是一个好的选择)。我们现在的交易策略如下:
仓位的计算公式:$-(y-movingAvg)/movingStd$,其中移动平均线和移动标准差的周期由均值回归的半衰期决定。也就是说,我们当前价格偏离移动平均线越多,我们就越往移动平均线方向交易(高于移动平均线就做空,低于移动平均线就做多)。
简单的回测代码:
lookback = 192
movingAvg = df_close.rolling(window=lookback).mean().dropna()
movingStd = df_close.rolling(window=lookback).std().dropna()
mktVal = -(df_close[-len(movingAvg):] - movingAvg) / movingStd
pnl = mktVal.shift(1) * (df_close[-len(mktVal):] - df_close[-len(mktVal):].shift(1)) / df_close[-len(mktVal):].shift(1)
回测结果:(策略代码过于冗长在此不放了)
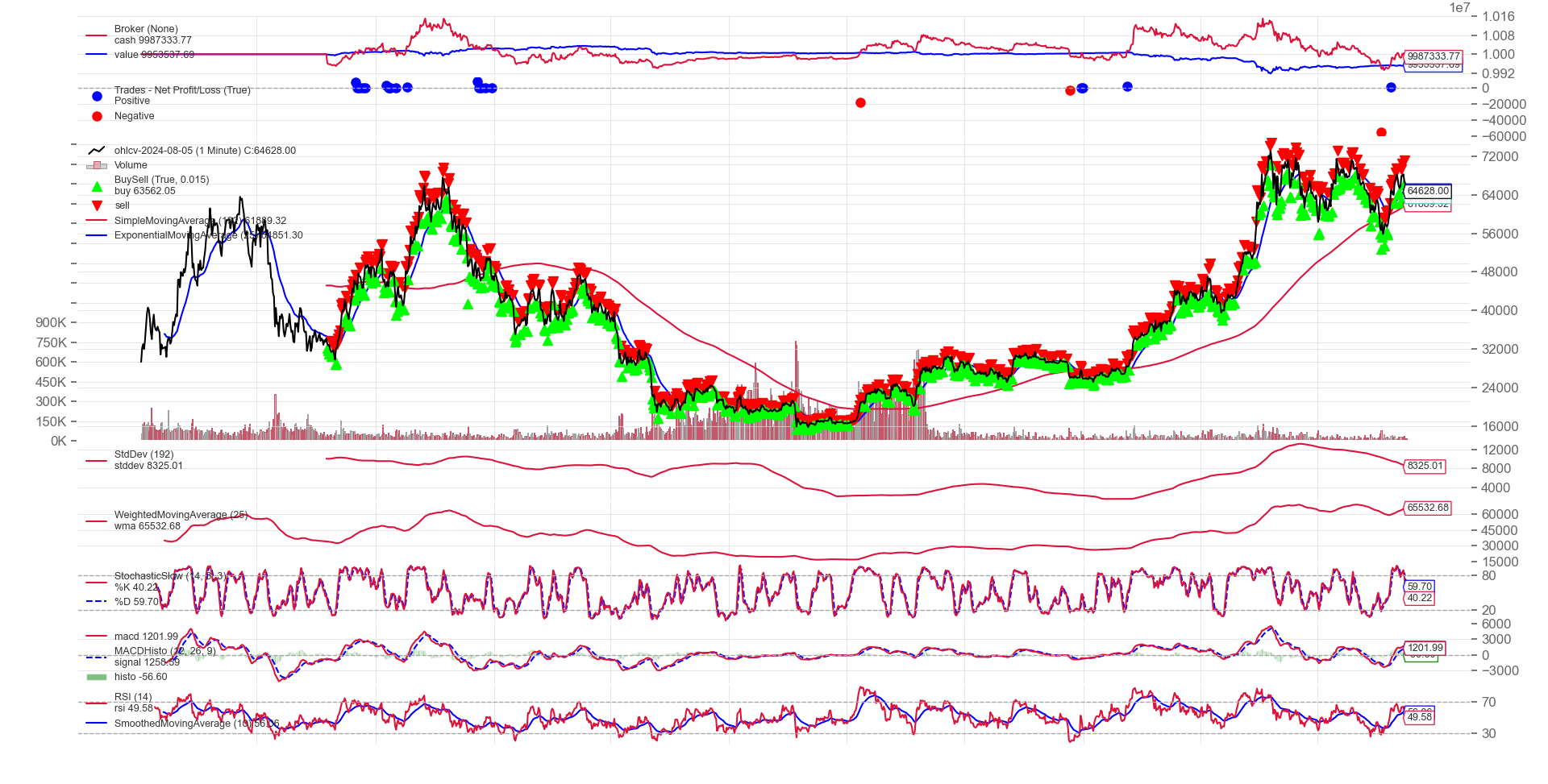
看出这个策略有什么问题了吗?
没错,就是前视偏差!我们使用所有的数据计算了均值回归的半衰期,然而,我们在交易时无法计算未来时间序列的半衰期。
上面的交易策略主要说明一个问题:一系列不平稳的价格不一定会阻止我们运行一个均值回归的交易策略,在向均值回归系统攫取利润的过程中,我们并不需要多么复杂的交易策略或者技术指标。
平稳测试后的协整
显而易见,大多数金融产品是不符合均值回归规律的。但我们可以同时交易多种资产!我们可以创建一个单独的价格序列组合,相应的市场价格是平稳的。
如此,则引出了协整的概念:如果我们可以找到一个由几个非平稳的价格序列所构建的平稳的线性组合,那么这个价格系列被称为协整形式。最常见的组合包含两个价格序列(我们在做多一种资产的同时,做空另一种资产,这就是我们所说的配对交易策略)。下面我们将介绍两个常见的协整性测试:加强对ADF检验(CADF)和约翰森检验。
扩展性迪基富勒检验模式
我们不是有了ADF检验吗?为什么还要这个加强的?这是因为:我们无法先验的决定该以什么样的对冲比例将两个资产组合在一起。一种可行的方法是:我们先根据两个价格序列之间的线性回归的相关性来确定最优的对冲比率,然后使用这种对冲比率的投资组合进行平稳性测试。
书上提到的CADF检验实际上就是Engel-Granger 两步协整检验法。我们可以使用statsmodels库中的coint函数来实现这个检验。
下面我们尝试检测比特币和以太坊的协整性:
我们先画图,从直观上观察他们的性质:
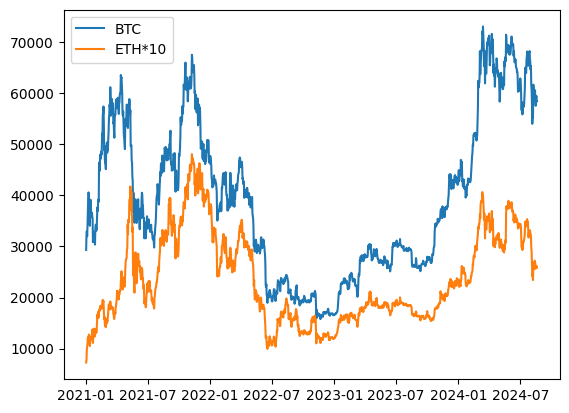
随后画出其散点图:
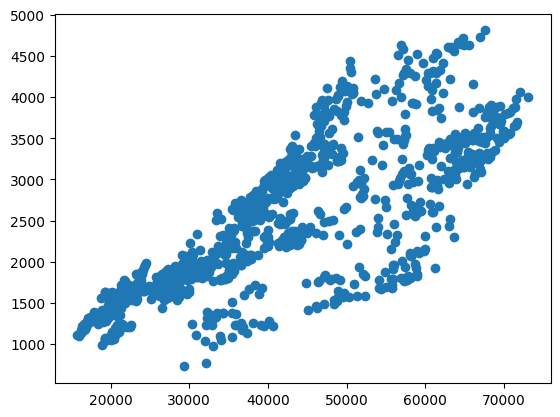
对其进行最小二乘拟合:
import statsmodels.api as sm
X = sm.add_constant(btc_close)
model = sm.OLS(eth_close, X)
res = model.fit()
hedge_ratio = res.params[1]
logging.info("OLS results: {}".format(res.summary()))
logging.info("Hedge ratio: {}".format(hedge_ratio))
得到结果:
OLS results: OLS Regression Results 2839918148.py:7
======================================================================
========
Dep. Variable: close R-squared:
0.669
Model: OLS Adj. R-squared:
0.669
Method: Least Squares F-statistic:
2673.
Date: Tue, 20 Aug 2024 Prob (F-statistic):
7.21e-320
Time: 00:46:53 Log-Likelihood:
-10139.
No. Observations: 1325 AIC:
2.028e+04
Df Residuals: 1323 BIC:
2.029e+04
Df Model: 1
Covariance Type: nonrobust
======================================================================
========
coef std err t P>|t| [0.025
0.975]
----------------------------------------------------------------------
--------
const 503.1567 38.383 13.109 0.000 427.858
578.455
close 0.0471 0.001 51.702 0.000 0.045
0.049
======================================================================
========
Omnibus: 37.097 Durbin-Watson:
0.017
Prob(Omnibus): 0.000 Jarque-Bera (JB):
79.867
Skew: -0.116 Prob(JB):
4.54e-18
Kurtosis: 4.180 Cond. No.
1.15e+05
======================================================================
========
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is
correctly specified.
[2] The condition number is large, 1.15e+05. This might indicate that
there are
strong multicollinearity or other numerical problems.
我们再调用statsmodel包中的协整性检验函数coint进行检验:
from statsmodels.tsa.stattools import coint
coint_t, p_value, critical_values = coint(btc_close, eth_close)
得到结果,只有0.45的概率能够拒绝非协整假设,所以btc和eth的价格序列是不够协整的。
约翰森检验
上一节,我们提到价格可以如下表示:
\[\Delta y(t) = \lambda y(t-1) + \mu + \beta t + \alpha_1 \Delta y(t - 1) + ... + \alpha_K \Delta y(t-k) + \epsilon_t\]然而,当我们有多个价格序列时,我们可以将其转化为向量和矩阵的表示形式:
\[\Delta Y(t) = \Lambda Y(t-1) + M + A_1 \Delta Y(t-1) + ... + A_K \Delta Y(t-k) + \epsilon_t\]我们需要检验的东西是矩阵\(\Lambda\)的秩\(r\)。如果\(\Lambda\)的秩为0,那么我们就可以拒绝非协整性假设。同时,由各种线性组合的投资标的组合的数量也等于\(r\)。进而我们可以进行测试是否\(r\)等于价格序列的个数\(n\)(若\(r<n\),说明不是所有资产组合中的资产都参与到这个协整过程中)
下面我们举一个例子:我们选择ADA, XRP, SOL三种币进行约翰森检验:
from statsmodels.tsa.vector_ar.vecm import coint_johansen
result = coint_johansen(np.array([ada_close, xrp_close, sol_close]).T, det_order=0, k_ar_diff=1)
print("Eigenvalues:", result.eig)
print("Eigenvectors:", result.evec)
print("Critical values (90%, 95%, 99%):", result.cvt)
print("Trace statistic:", result.lr1)
print("Max eigenvalue statistic:", result.lr2)
输出:
Eigenvalues: [0.01556343 0.00747861 0.0052115 ]
Eigenvectors: [[ 1.55284363 -0.43703663 -2.47380391]
[-6.10182014 -0.84906992 2.41205223]
[ 0.00906315 -0.01161473 0.01089735]]
Critical values (90%, 95%, 99%): [[27.0669 29.7961 35.4628]
[13.4294 15.4943 19.9349]
[ 2.7055 3.8415 6.6349]]
Trace statistic: [37.62498993 16.85697239 6.91807507]
Max eigenvalue statistic: [20.76801754 9.93889731 6.91807507]
可以看到,有迹检验量和最大特征值检验量。从迹检验量来看,有95%的把握认为这三种币存在协整关系。然而,从最大特征值检验量来看,我们的把握就小的多了。同时,约翰森检验也给出了特征向量和特征值。显然,第一个特征值最大,那么我们可以认为第一组协整关系是最强的,也就是说,我们可以选择三个特征向量中的第一个作为我们的投资组合比例分配。
下面我们根据特征向量构造的投资组合进行半衰期的计算:
jigen_vector = [1.55284363, -6.10182014, 0.00906315]
triple_price_series = np.array([ada_close, xrp_close, sol_close])
spread = np.dot(eigen_vector, triple_price_series)
plt.plot(spread)
plt.show()
spread_series = pd.Series(spread)
ylag = spread_series.shift(1)
deltaY = spread_series - ylag
deltaY = deltaY[1:]
ylag = ylag[1:]
X = sm.add_constant(ylag)
regress_results = sm.OLS(deltaY, X).fit()
half_life = -np.log(2) / regress_results.params[0]
得到投资组合的净值曲线:
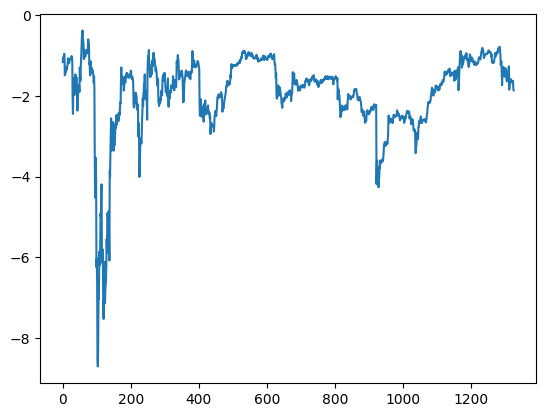
计算得到半衰期为29.97天。这个半衰期比之前单一资产的半衰期短的多,使得我们有机可乘!
投资组合相关的线性均值回归交易模式
同样的,我们用一个十分简陋、不切实际的策略进行回测,即我们的仓位和(投资组合净值的偏离程度/投资组合净值的标准差)成正比。我们就使用上述的三种币的投资组合进行回测。
策略主体部分节选:
def __init__(self):
# Keep a reference of the "close line" in the datas[0]
self.dataclose = self.datas[0].close
# Keep a track of orders and buy price/commission
self.order = None
self.buyprice = None
self.buycomm = None
self.yport = self.params.eigen_vector[0] * self.datas[0].close + \
self.params.eigen_vector[1] * self.datas[1].close + \
self.params.eigen_vector[2] * self.datas[2].close
# Add a MovingAverageSimple indicator
self.sma = btind.SimpleMovingAverage(
self.yport, period=self.params.maperiod)
self.smstd = btind.StdDev(self.yport, period=self.params.maperiod)
def next(self):
self.log("Close, {:.2f}".format(self.dataclose[0]), doprint=True)
self.num_units = -(self.yport[0] - self.sma[0]) * 10000 / self.smstd[0]
if self.order:
return
positions = []
for i, data in enumerate(self.datas):
weight = self.params.eigen_vector[i]
position = self.num_units * weight * data.close[0]
positions.append(position)
self.order_target_value(data, position)
回测结果:
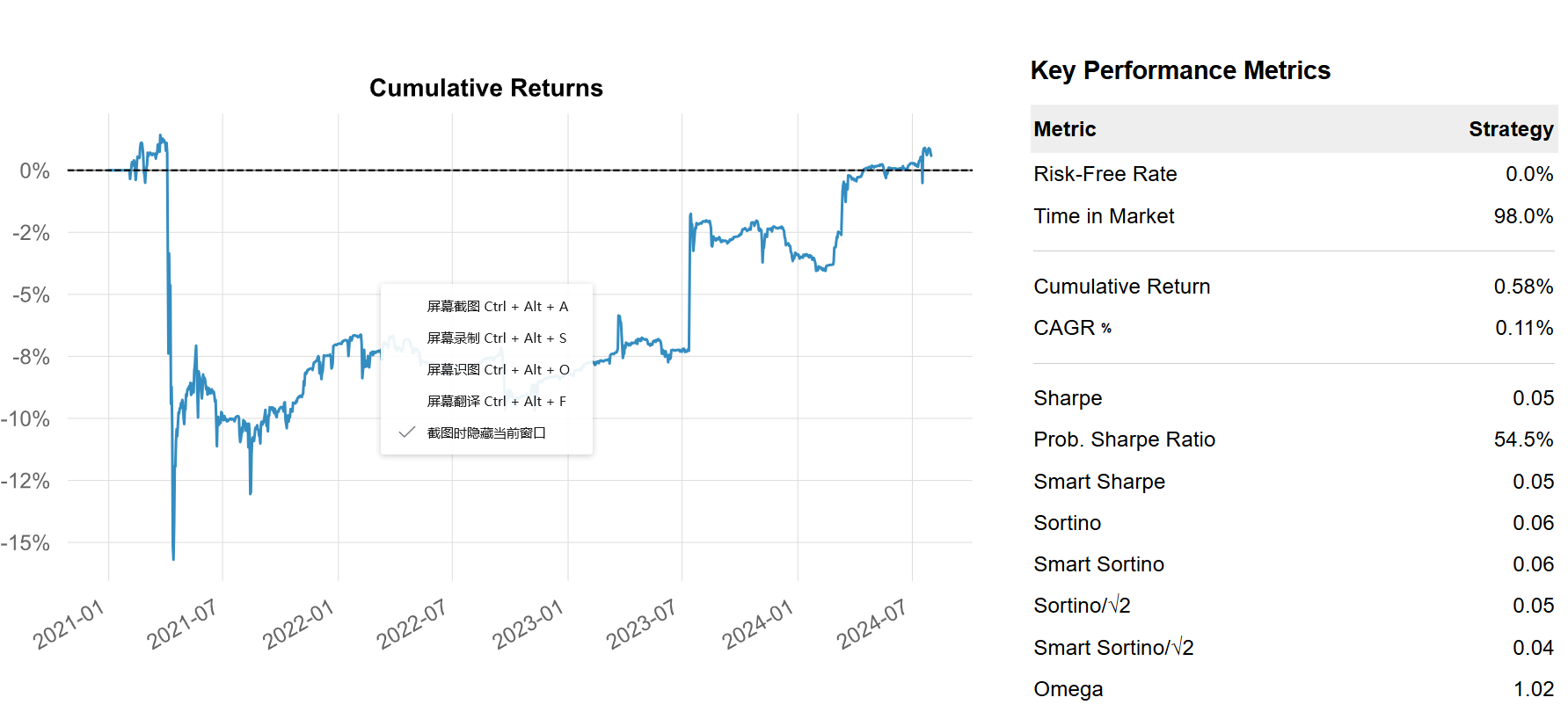
可以看到,十分的拉胯。笔者以为,这是因为这三个币从逻辑上来看并不具有十分强烈的协整性关系,当价差过大的时候,可能会遭受巨大的亏损。一般价差趋势来到如此强烈的地步,我们就应该思考,这个投资组合是否还是协整关系?这也告诉我们一个重要的道理:有时候检验统计量并不是如此的可靠!
总结:均值回归策略的利弊分析
均值回归的几个优点:
- 我们可以自由的创建自己的投资组合。当然,在crypto领域,这种投资组合的机会可能并不多,这种均值回归的策略应该更适合ETF的交易策略。
- 均值回归策略跨越了各种规模的时间尺度。均值回归的半衰期从几天到几年各不相等,当然我们认为半衰期越短的交易策略对我们更好。
不幸的是:看似具有很高一致性的均值回归交易策略最终很有可能失效!巨大的亏损常常发生在策略取得一系列成功之后,加大交易杠杆的时候,由此产生的罕见损失往往十分痛苦!因此,风险管理的概念显得十分重要。