写在前面：本文仅供学习交流使用，不构成任何投资建议！

前言

量化交易的两种基本模式是：均值回归和趋势。前者的意思是价格序列大致维持平稳，这样我们可以根据当前价格偏离平稳价格的多少进行相应的做多或做空。后者的意思是判断当前价格序列的趋势，这样我们顺势而为即可。本节我们探索均值回归模式。

均值回归和平稳性，在时间序列类型和时间序列表现上是两种相同的方法。然而，这两个名词产生了不同的统计检验方法：

• 均值回归模式的数学表达：价格序列的变化在未来与当前价格和均值水平之差成正比。对应ADF检验
• 平稳性的数学表达：价格的波动方差的增长速度要低于几何形式的随机波动速度。也就是说，价格序列纵向扩散到速度小于随机波动（布尔运动）。对应Hurst指数检验和方差比检验。

本文主要参考资料：”Algorithmic Trading: Winning Strategies and Their Rationale”, Ernest P. Chan

ADF检验

均值回归型 –> 当前的价格水平将会告诉我们下一步的运行情况如何。如果价格水平高于均值，那么价格将会下降。如果价格水平低于均值，那么价格将会上升。ADF检验就是基于这个假设进行观测的。

我们可以将价格的变化以线性的形式表示出来：
\(\Delta y(t) = \lambda y(t-1) + \mu + \beta t + \alpha_1 \Delta y(t - 1) + ... + \alpha_K \Delta y(t-k) + \epsilon_t\)

其中，\(\Delta y(t)\)是价格的变化，\(y(t-1)\)是上一时刻的价格，\(\mu\)是均值，\(\beta t\)是时间趋势，\(\alpha_1 \Delta y(t - 1)\)是上一时刻的价格变化，\(\epsilon_t\)是误差项。

如果\(\lambda = 0\)，那么ADF检验生效，说明价格的变化和此时的价格无关。若\(\lambda = 0\)的假设被拒绝，说明价格的变化和此时的价格有关，价格序列不是随机游走的.

更详细的一些解释：我们的检验统计量使用\(\lambda / SE(\lambda)\)（SE：标准差）。Dickey, Fuller等人为我们发现了这个检验统计量的临界值。除此而外，临界值还依赖于：我们是否认为价格序列有一个非零的均值(\(\mu / \lambda\))，以及一个稳定的漂移率(\(\beta t/ \lambda\))。

ADF检验的python代码：这里我们以比特币的近三年日线数据为例，检验其是否为均值回归模式。

df = pd.read_csv(dataset_path)
df['date'] = pd.to_datetime(df['candle_begin_time_GMT8'])
df.set_index("date", inplace = True)
df_close = df["close"]
plt.plot(df_close)
plt.show()

result = adfuller(df_close) 
logging.info(result)
logging.info("ADF Statistic: {}".format(result[0]))
logging.info("p-value: {}".format(result[1]))
for key, value in result[4].items():
    logging.info("Critical Values {}: {}".format(key, value))

走势图：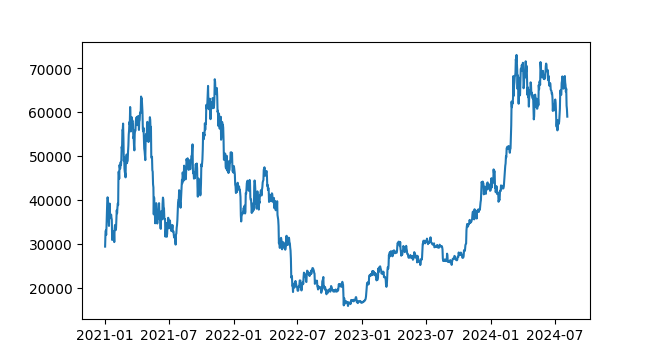

检验结果：

INFO     ADF Statistic: -1.3011773213938496         
INFO     p-value: 0.6286335157234405                
INFO     Critical Values 1%: -3.435359311744588     
INFO     Critical Values 5%: -2.863752202145595     
INFO     Critical Values 10%: -2.5679477886494775     

检验结果显示，其ADF检验统计量值为-1.3，而最下方的三个数值对应相应置信度的临界值。例如，统计量的值必须小于-3.43才能有99%的把握拒绝\(\lambda = 0\)的假设。此处可见，并没有多少把握可以拒绝非平稳的假设。（*Note: 为什么ADF检验统计量是负的? 可以直观的理解，在均值回归模式下，如果价格过高，下一个价格应当降低，反之亦然，所以此时\(\lambda\)不可能是正的，这样价格越高，下一个价格就趋向于更高。

平稳性检验（Hurst指数检验与方差比检验）

Hurst指数

平稳的价格序列意味着价格扩散的速度比几何随机游走的扩散速度更慢：那么我们可以通过测量价格扩散到速度来确定价格序列的性质。而价格扩散的速度可以用方差来表示：
\(\mathrm{Var}(\tau)=\left\langle\left|z(t+\tau)-z(t)\right|^2\right\rangle\)
其中，\(\tau\)表示任意的时间延迟，\(z=log(y)\)对数价格，\(\left\langle ... \right\rangle\)表示所有时间序列之和。
对于随机游走序列，有：
\(\mathrm{Var}(\tau)=\left\langle\left|z(t+\tau)-z(t)\right|^2\right\rangle \sim \tau\)
当\(\tau\)较大的时候，上述比例关系更加成立; \(\tau\)较小的时候，可能会偏离线性关系。
而倘若价格序列有均值回归或者趋势性，那么我可需要改写：
\(\mathrm{Var}(\tau)=\left\langle\left|z(t+\tau)-z(t)\right|^2\right\rangle \sim \tau^{2H}\)
赫斯特指数即为\(H\)：

• \(H\)=0.5：表示时间序列可以用随机游走(布朗运动)来描述。
• 0<\(H\)<0.5：表示记忆的转弱(反持续性)，即均值回复过程。
• 0.5<\(H\)<1：表示记忆增强(持续性)，即暗示长期记忆的时间序列。

代码：（以比特币为例）

from hurst import compute_Hc    
H, c, data = compute_Hc(df_close, kind='random_walk')
logging.info("Hurst exponent: {}".format(H))

输出：

Hurst exponent: 0.5145450110647813 

得到的Hurst指数接近0.5，说明比特币价格走势接近于随机游走。

此处我们直接调包使用，具体计算方法我们在此不作深入探究。

方差比检验

方差比检验验证的是\(\mathrm{Var}(z(t) - z(t - \tau))/ \tau \mathrm{Var}(z(t) - z(t - 1))\)的值是否等于1. 由随机游走的性质可以知道，时间序列的方差与时间跨度成正比。代码如下：

from arch.unitroot import VarianceRatio
vr_test = VarianceRatio(df_close, lags=3)
logging.info(vr_test)

这里我们直接调用arch包。值得注意的是，lags参数设置的不同，对结果影响很大。例如，我们使用默认的参数lags=2，那么给出的结果是：

Variance-Ratio Test Results     
=====================================
Test Statistic                 -1.616
P-value                         0.106
Lags                                2
-------------------------------------

Computed with overlapping blocks (de-biased)

这里p-value的值代表零假设检验（随机游走）是正确的概率。当我们设置lags(\(\tau\))=2时，显示只有0.106的概率是随机游走。当我们设置lags=5:

      Variance-Ratio Test Results     
=====================================
Test Statistic                 -0.619
P-value                         0.536
Lags                                5
-------------------------------------

此时有0.536的概率接受假设，所以我们不能断定比特币走势是非随机游走的。这种方法对lags的选择比较敏感，所以我们需要其他检验统计方法共同决策。

均值回归的半衰期

实际交易中，我们很难碰到具有很高置信度的平稳性的价格序列（例如置信度达到90%以上）。但实际交易中，我们未必需要如此严苛的条件才能实现盈利。回忆我们前面提到的价格关于时间的表达式：

\[\Delta y(t) = \lambda y(t-1) + \mu + \beta t + \alpha_1 \Delta y(t - 1) + ... + \alpha_K \Delta y(t-k) + \epsilon_t\]

在前面的统计检验中，我们直接决定\(\lambda\)取0还是1. 我们现在可以设法让\(\lambda\)取值在0-1之间，相应的解释是\(\lambda\)主要测量价格到底需要多长时间才能恢复到均值回归的水平。

我们将上式进行微分，得到：

\[dy(t) = (\lambda y(t-1) + \mu)dt + d \epsilon\]

这里的解释是，我们前面的式子左侧\(\Delta y(t)\)取得是t相差1时的斜率，而我们现在可以让t作为一个微分。

我们可以使用线性回归的方式，由第一个式子得到\(\lambda\)的值，确定这个值后，我们将其代入第二个式子，而由相应的偏微分方程可以得到\(y(t)\)的期望值：

\[E[y(t)] = y_0 exp(\lambda t) - \mu / \lambda [1 - exp(\lambda t)]\]

(这里我还没推出来…数学基础有点差)

这里我们需要记住：\(\lambda\)为负数时，均值回归的过程才成立。相应价格指数衰减的期望值为\(-\mu / \lambda\)，衰变的半衰期为\(- log(2) / \lambda\)。用\(\lambda\)求半衰期很有用：

1. 若\(\lambda\)是正数，那么说明不是均值回归的形态。
2. 若\(\lambda\)非常接近于0，说明半衰期过长，均值回归的交易策略不会很赚钱（我们在同样时间内完成交易的次数会变少）。
3. 若\(\lambda\)可以帮助我们决定策略中的一些参数。例如我们测得半衰期为20天，就不应该用5天的移动平均线。

在计算时，我们设置一个回归方程，自变量为\(y(t-1)\)，因变量为\(y(t)-y(t-1)\)，随后使用最小二乘法对其进行线性回归。

python代码：

import statsmodels.api as sm
df_close_lag = df_close.shift(1)
df_close_lag = df_close_lag.dropna()
delta_df_close = df_close[1:] - df_close_lag
# 添加常数项
df_close_lag2 = sm.add_constant(df_close_lag)
# 最小二乘法
model = sm.OLS(delta_df_close, df_close_lag2)
res = model.fit()
halflife = round(-np.log(2) / list(res.params)[1],0)
logging.info("Halflife: {}".format(halflife))

对Bitcoin价格序列进行计算得到的结果为192天。这个半衰期很长，说明比特币并不是很适合进行均值回归的交易策略，但也至少可以让我们对回测以及持仓的期限有所预期。

总结

以上我们大致介绍了书里面提到的几种检验价格序列平稳性和均值回归属性的方法。下一节我们将介绍一些简单的均值回归交易策略以及回测。